Ringel は triangulation の 2 つの性質を指摘した。
- は局所的にハミルトニアン (locally Hamiltonian) である。つまりそれぞれの頂点 について、 の近傍で誘導されるグラフ は ハミルトンサイクルを持つ。
- を辺数、 を面の数としたとき、 だからオイラーの公式より、 は 3 で割り切れる非負整数である。( より )
Ringel はこの 2 つの条件は triangulation となるために十分な条件ではないことも指摘した。
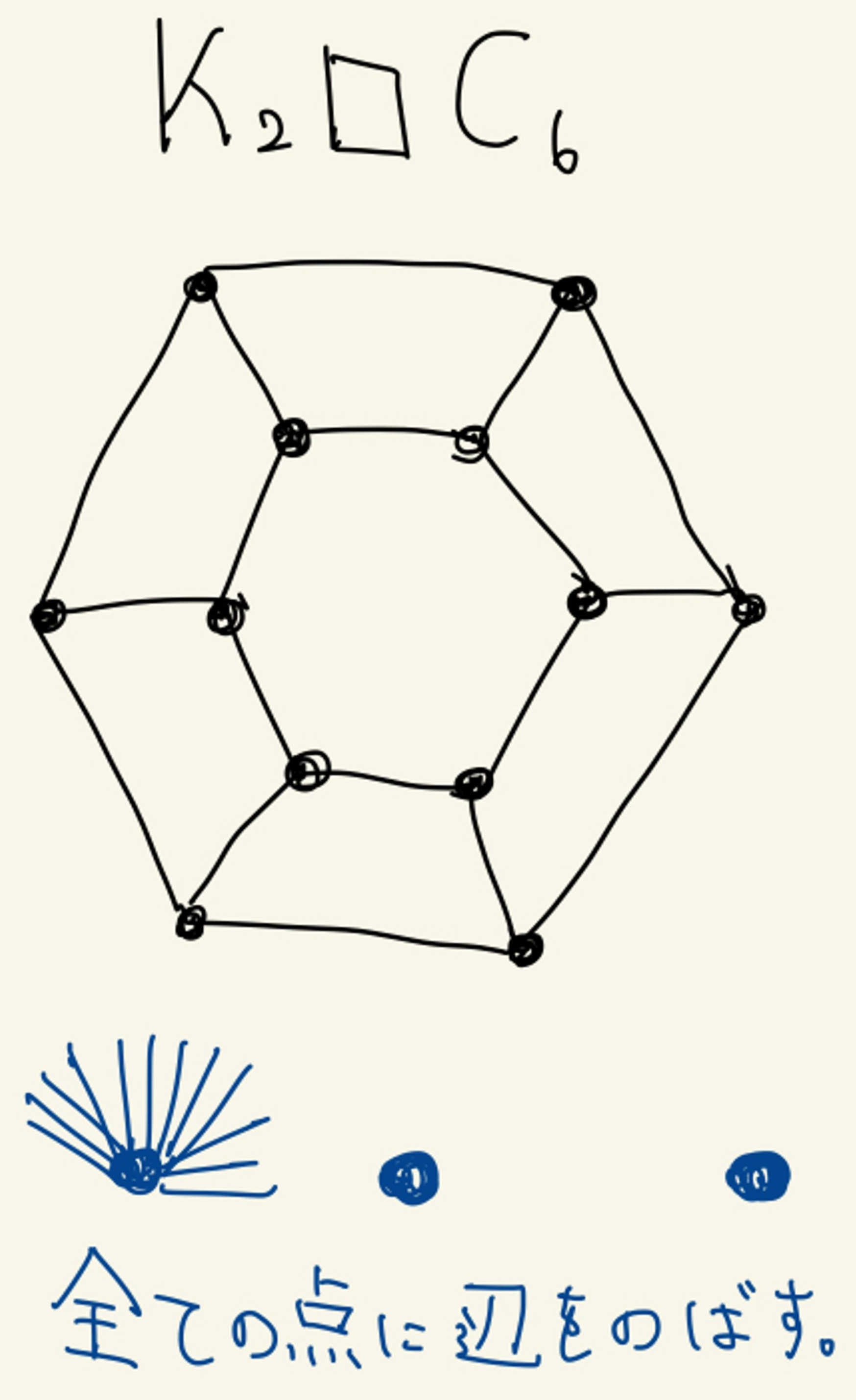
実際に定理 4.4.9 は 2 つの必要条件を満たすものの、triangulation ではないようなグラフの多くの例を与える。より簡単な例も Thomassen により挙げられている。例えば、プリズムグラフ に新しい頂点を 3 つ付け足し、その 3 頂点から の全ての頂点に辺を張ったグラフ は triangulation ではないことが示されているが、 2 つの必要条件を満たす。
補題 2.3.3 から球面上の triangulation は 3 連結であることがわかるが、以下の命題 5.3.1 は任意の曲面の triangulation も 3 連結であることを主張する。
命題 5.3.1 (Thomassen)
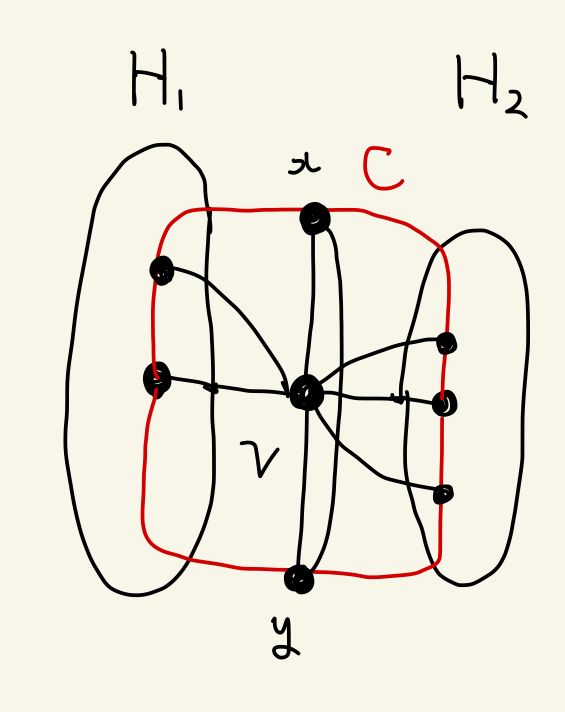
を連結な局所ハミルトニアンとする。このとき は 3 連結である。さらに、 が の separating set なら、 は 3 サイクル を含み、 は のどのハミルトンサイクルの辺でもない。 はちょうど 2 つの連結成分 をもち、 は局所ハミルトニアンである。
証明
を smallest separating set としたとき、 は の全ての連結成分に辺を伸ばしているから、 がハミルトンサイクル を持っていることを考えると、 には 以外に少なくとも 2 頂点は必要だから、 である。
としたとき、 はちょうど 2 つの連結成分 を持つ。( が 2 つの連結成分からなっているから)、そして、 は の近傍でなければならない。 についても同様に考えると、 は の近傍でなければならない。つまり は 3 サイクルである。また は のコードであり、ハミルトンサイクルの辺ではない。
が局所ハミルトニアンであることと が 3 サイクルをなしていることから も局所ハミルトニアンであることがわかる 。
次の結果は edge-width が 4 以上の場合の Ringel の疑問の答えになっている。
定理 5.3.2(Thomassen)
を連結グラフとする。 が長さ 3 の noncontractible サイクルを持たない triangulation なら、
- は局所ハミルトニアン、
- の全ての辺はちょうど 2 つの nonseparating 3-cycle に含まれている、
が成り立つ。逆に が 1, 2 の両方を満たすなら、 はある曲面を triangulate する。
証明
triangulation なら 1 を満たすことは自明。さらに の辺は 2 つの 3-facial サイクルに含まれており、定理 5.1.5 からそのサイクルは nonseparating である。それ以外の nonseparating 3-cycle に含まれているとするとそれは noncontractible だから、矛盾する。
逆に、1, 2 を満たすとする。任意の は以下の条件を満たすハミルトンサイクル をただ一つもつ: を含む nonseparating 3 サイクルの集合と が一致する。
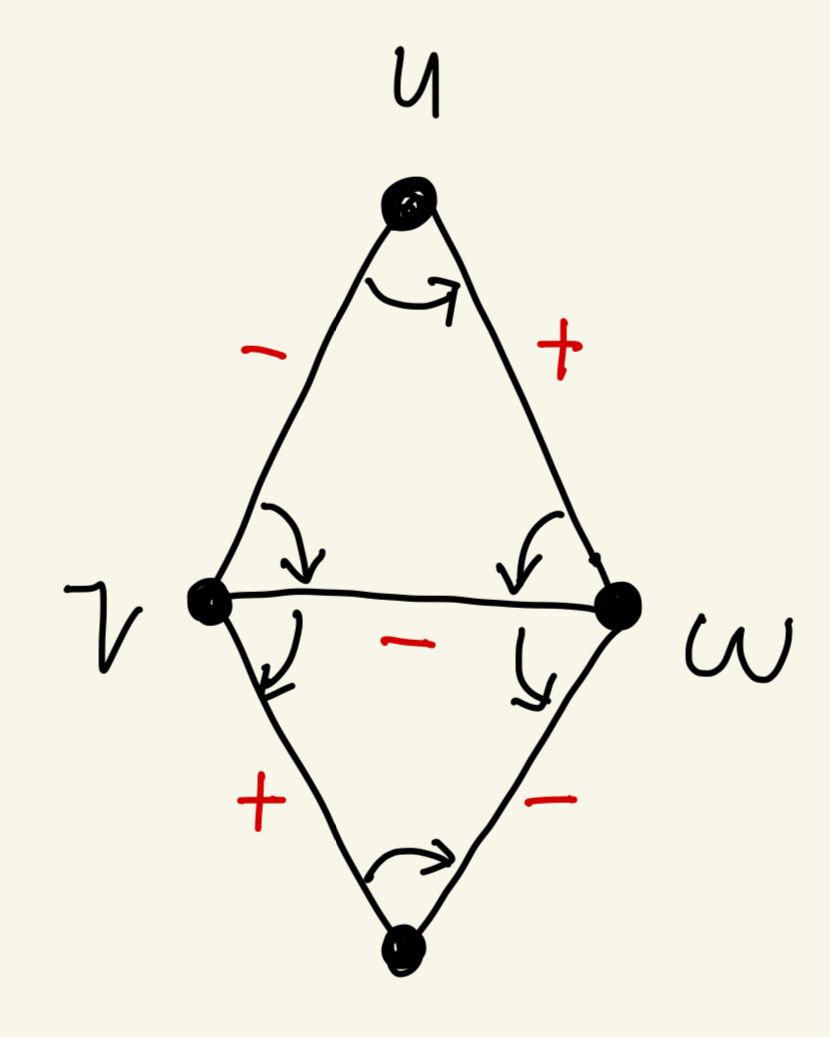
このサイクル を の rotation とする。適切に辺の符号を決めれば (下のように rotation が一致していないときに - をつけて、そうでないときに + をつける)、facial walk が nonseparating 3 サイクルであるような triangulation になる。
定理 5.3.2 の条件 1, 2 は が surface nonseparating 3-cycle を持たない 3 角形分割を持つ必要十分条件であることも示せる。
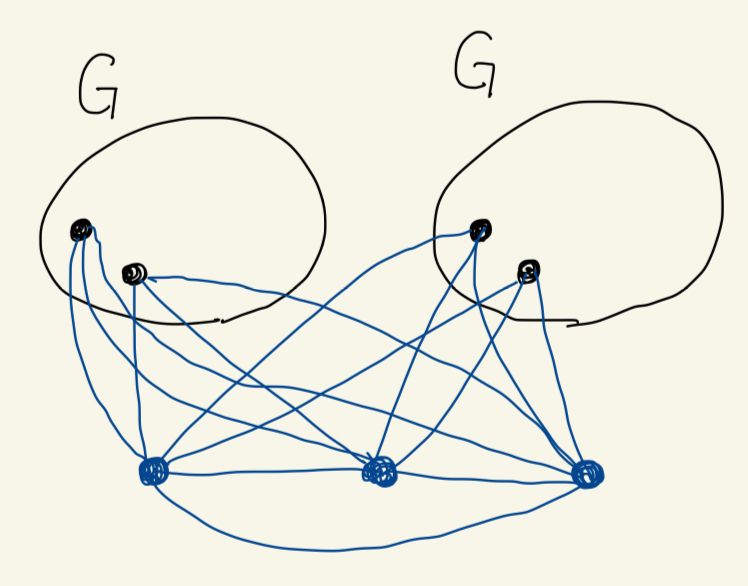
以下のようにすると 3 正則グラフがハミルトンパスを持つかを決定するという NP 完全な問題を局所ハミルトニアンかどうかを決定する問題に帰着することができる: 3 正則グラフ をとってきて、 の 2 つのコピーを作り、3 つの新しい頂点とそれらの頂点を他の全ての頂点に隣接させる。このようにしてできたグラフが局所ハミルトニアンであることと、 がハミルトンパスを持つことは同値である。
同値であることの説明
ハミルトンパス → 局所ハミルトニアン: 元々 に存在していた頂点 については 3 正則だから、新しく足した 3 頂点を使えば、近傍にハミルトンサイクルが得られる。新しく付け足した頂点 ( とする)については のハミルトンパスを として ( に含まれる ) → → ( のコピーに含まれる → の順に回れば の近傍のハミルトンサイクルが得られる。 も同様。
局所ハミルトニアン → ハミルトンパス: 上と同様
つまりグラフが局所ハミルトニアンであることを決定する問題も NP 完全である。一方、定理 5.3.2 の 2 の条件のチェックは簡単である。さらに次の命題 5.3.3 に見るように 2 を満たすグラフについては、 1 の条件は平面性判定アルゴリズム (つまり多項式時間で!) で判定することができる。
命題 5.3.3 (Thomassen)
を定理 5.3.2 の性質 2 を満たす連結グラフとする。このとき が性質 1 を満たすことと全ての closed neighborfood graph が 3 連結で平面的であることと同値である。
証明
が 3 連結で平面的だから、その平面描画で を取り除いてできた (2 連結) の面の facial cycle がハミルトンサイクルになっている。
逆に が局所ハミルトニアンであったとする。 をとって、 を のハミルトンサイクルとする。定理 5.3.1 (separating set について、 の近傍のハミルトンサイクルには辺 は含まれない) より と の辺を使った 3 角形は nonseparating である。
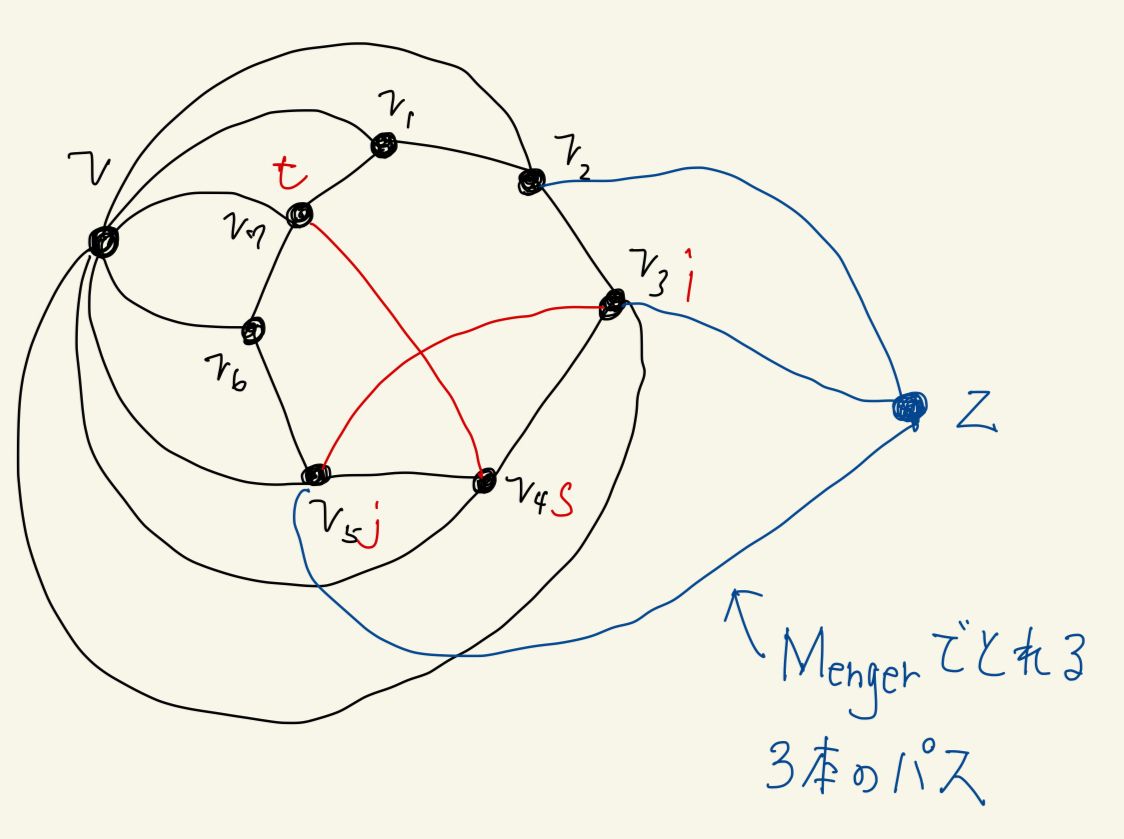
下の図のように を凸多角形、 を の外側に描く。 に存在している のコードを全て内側に直線で描く。この埋め込みが の平面への埋め込みになっていることを示す。 と が交わっているとすると、辺 はすでに と という nonseparating 3 サイクルに含まれているから性質 2 を満たすという仮定より は separating でなければならない。 は命題 5.3.1 より 3 連結であるから、Menger の定理より の任意の頂点 と の間に 3 本の disjoint なパスをもつ。このことから のある頂点から へ伸びるパスが存在する。よって、 において、 の 2 つのパスが辺 で結ばれていることを考えると、 は連結である。これは が separating であったことに矛盾する。
Lavrenchenko は短い noncontractible サイクルを持たないトーラス上の triangulation はトーラス上にユニークに埋め込めるかどうかを考えた。次の結果はその問題の拡張と見なせる。
定理 5.3.4 (Thomassen)
-embedded グラフ が triangulation であり、かつ が以下の 2 つの条件のうちいずれかを満たすなら、 は の最小オイラー種数の曲面へのただ一つの埋め込みになっている。
- は -noncontractible かつ nonseparating な 3 サイクルを持たない。
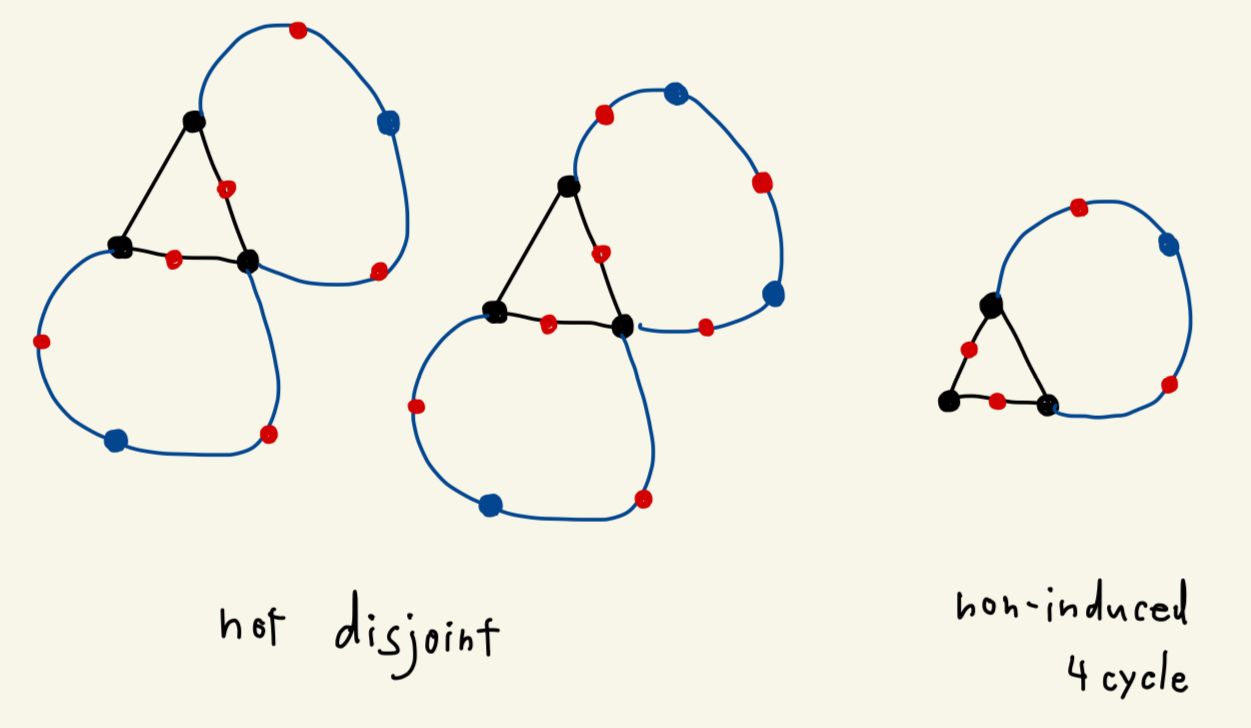
- どの -noncontractible な 3 サイクル, induced -noncontractible 4 サイクルどうしも disjoint である。
証明
が 1 を満たすとする。 が と同じオイラー種数を持つ埋め込みとする。同じオイラー種数を持つことから もまた triangulation である。よって全ての -facial 3 サイクル が -facial でもあることを示せば良い。命題 5.3.1 ( の近傍のハミルトンサイクルに含まれる辺 があると は nonseparating である) より は nonseparating である。よって条件 1 より は -contractible である。よって は -facial である。つまり が成り立つ。
が 2 を満たすとする。 の -noncontractible な 3 サイクル、induced -noncontractible な 4 サイクルに含まれる辺に次数 2 の頂点を一つ加えて subdivide する。できたグラフ は edge-width が 5 以上で、全ての facial cycle の長さが 4 以下である。
よって LEW である。定理 5.2.2 を使う。
